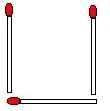
Jouons avec des allumettes :
1. Avec trois allumettes disposés comme ceci, faites un carré en n'en déplaçant qu'une seule.

2. Sept allumettes sont disposées de la manière suivante:
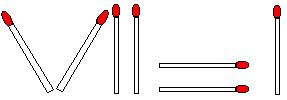
3. Avec 11 allumettes dessiner un petit cochon comme sur la fugure ci-dessous:
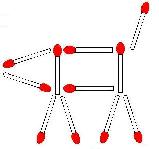
4. Ces 8 allumettes dessinent un poisson qui nage de droite à gauche.
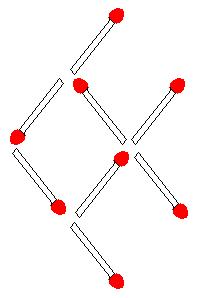
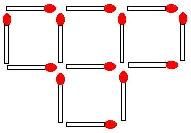
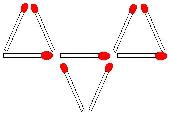
5. Sur la figure1, déplacez trois allumettes pour construire une nouvelle figure contenant cinq carrés.
Sur la figure 2, déplacez quatre allumettes pour construire une nouvelle figure contenant cinq triangles.
Jouons avec des pièces de monnaie :
Six pièces de monnaie sont disposées en triangle de la mannière suivante :

Jouons avec des billes :
Quatre billes rouges et quatre billes bleues sont disposées de la façon suivante :

Promenons-nous sur un réseau :
Dans le réseau ci-dessous, on part du point D pour atteindre le point A (les points sont aux intersections en bas à gauche des limites des cellules).
On se déplace sur les lignes et deux direction sont autorisées :
- de gauche à droite
- de bas en haut
Combien de chemins différents existe-t-il pour ce déplacement ?
| A | |||||||
| D |
Diagramme du prisonnier :
Dans la prison représentée ci-dessous, le prisonnier X devient fou ; il casse le mur de la cellule voisine et tue le prisonnier qui s'y trouve. Sachant qu'il y a un prisonnier par cellule, qu'après chaque assassinat il abandonne la victime pour en chercher une autre, qu'il ne retourne jamais dans une cellule où se trouve un cadavre, qu'il tue tous les prisonniers et qu'il ne casse jamais un mur extérieur ou le coin entre les cloisons d'une cellule, quel est son itinéraire macabre sachant que le dernier prisonnier tué est le O ?
| X | |||
| O |